
Innovations in Pulse Fidelity for
High-Power GaN Radar and EW Transmitters

L Band 40 kW
Pulsed Transmitter
Authors
- Darren Miles, Empower RF Systems
- George Bollendorf, Empower RF Systems
- Bob Buxton, Boonton Electronics
Introduction
This article discusses the correction of pulse droop and rising edge overshoot with data from Empower’s 40 kW L band long duty cycle liquid cooled pulsed amplifier, Model 2237, shown in figure1.
Radar and electronic warfare (EW) have been the primary applications for extremely high-power transmitters, driving the demand for specialized high-power traveling wave tubes (TWTs) and magnetrons. Diminishing sources of TWT supplies, with their poor reliability, inefficiency, large size, and high total lifetime cost of ownership, are causing the migration away from tubes. Improved pulse fidelity came along with the solid-state transmitter; however, next-generation radar depends on further improvements in waveform fidelity and flexibility.
For example, next-generation radar systems utilize long pulse widths, which present specific challenges. As a result, Empower RF has developed technology to reduce pulse distortion as a development step towards pulse shape matching – the reproduction of the input pulse without distortion. The pulse correction is performed within the amplifier in real time. Why is this important? Long pulse width radar is especially vulnerable to over/undershoot and droop, which can be eliminated thereby extending radar range and reducing receiver target acquisition time. The benefits from an EW perspective are the ability to accurately mimic adversarial pulses without pre-processing, allowing precise threat simulation and spoofing.

The Primary Cause of Droop in Solid-State Power Amplifiers
The primary cause of droop in a GaN power amplifier is the thermal response of the transistor. GaN has an inverse gain relationship with temperature. The thermal response of the transistors reduces the gain by 0.5 dB to 1.0 dB, depending on the temperature rise during the pulse. The droop is compounded with cascaded transistors resulting in a further reduction in output power. This is summarized in figure 2. The second contribution relates to a power supply’s ability to source current at high frequency. During the pulse, capacitive energy across the drain of the transistor is being discharged. This starts at the leading edge of the pulse and, as the pulse progresses to the trailing edge, the gain is increasingly reduced by the resulting drop in drain current and drain voltage. These two factors can account for up to 3 dB of droop. Fixing the droop in software allows a reduction in size and complexity of the power supply and increases average transmit power. The result is improved SWaP, cost, and MTBF.
Pulse Parameters and Impact on Radar Performance
Pulse droop is defined as the distortion of a flat-topped rectangular pulse, characterized by a decline of the pulse top. Figure 3 describes the characteristics of a pulsed signal. Generally, each pulse includes an overshoot and ripple at the leading edge of the pulse and a pulse droop, which is the reduction in the amplitude between the beginning and end of the pulse.
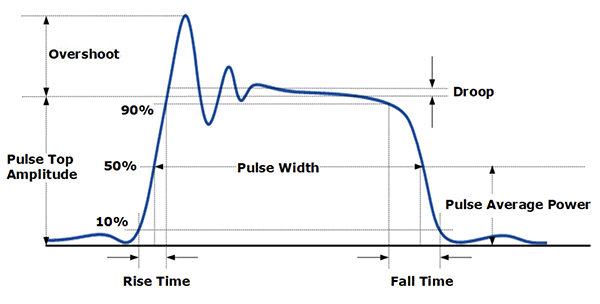
Let’s consider the impact of overshoot and droop on radar performance. A radar transmitter will have a limiter to protect the amplifier output stages from exceeding peak power ratings. When overshoot is present, the gain must be set so the overshoot of the pulse does not trip the limiter. When overshoot is absent or minimized, the amplifier output can be set just shy of the limiter threshold. In the case of droop, the power during the pulse is dropping over time, further reducing the average power. By examining the radar range equation, the impact of reduced power can be seen.
Where:
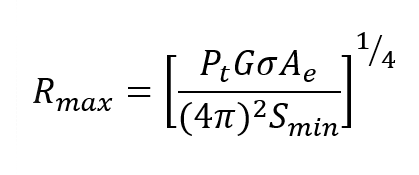
Rmax = the maximum range
Pt = the transmitter power
G = the transmitter antenna gain
σ = the target’s radar cross section
Ae = the receive antenna effective aperture
Smin = the minimum detectable signal
Assuming all other terms remain constant, the maximum range varies as the fourth root of the transmitter power. For example, a 1 dB improvement in average power increases the range by 6%.
Pulse Corrections
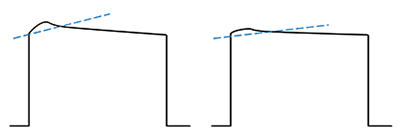
Each of the two main sources of droop have repeatable responses, in time, marked from each leading edge of the pulse. With fast enough sample rates, an algorithmic solution exists where the amplifier gain can be changed throughout the pulse in real time.
As an example, let’s take the simplest form of the algorithm. Since the junction temperature rate of change is highest on the rising edge when the transistor is turning on and conducting, the adjustment to the gain at the beginning of the pulse must be greater than during the body of the pulse. When this is accomplished, the result is a significant reduction in overshoot. After the overshoot section, a second element, gain adjustment of the algorithm, is employed. The math is pretty simple. The droop has a slope, so the gain adjustment simply adds in the inverse gain slope. The algorithm applied repeats itself with each pulse. This two-step algorithm can be further refined by adding more adjustment points; however, results of a two-stage correction by itself are very good and are shown below. The correction algorithm resides in FPGA firmware and is comprised of a finite state machine (FSM) described in HDL. The correction algorithm is configured with the appropriate parameters from a digital calibration process performed at the factory. The parameters include the slopes of the two-stage corrections and the initial power level amounts at the leading edge of the pulse.
Test Setup
For demonstration, an Empower amplifier is fed with a 1.5 GHz, 500 µsec pulse, nominally at 0 dBm. A separate guard band input is used to frame the pulse for operating in true pulse mode. The amplifier is set to full gain, achieving 40 kW peak at the output. The overall setup is shown in figure 5.
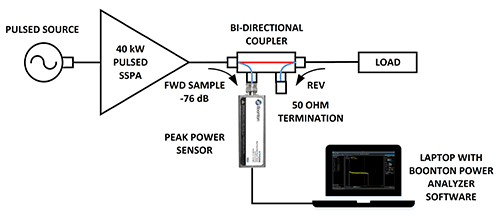

The amplifier has a bi-directional coupler at the output as seen in figure 6. The coupling factor is 76 dB. A Boonton RTP5006 USB Real-Time Peak Power Sensor was used; this is the only sensor fast enough to capture the peak of the overshoot. The full power is dumped into a 50-ohm load.
Results of Practical Implementation
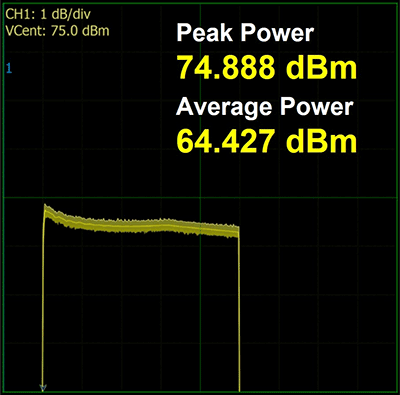
Figure 7 shows the measurement with the Boonton power sensor of the initial SSPA output before the correction algorithm is applied. This was captured by the Boonton Power Analyzer software. The peak with overshoot measures 76.1 dBm. The end of the pulse top is measured at 74.4 dBm. The Boonton software captures the pulse envelope and is able to export it to a CSV table. From that table, the overshoot can be determined to settle around 75.2 dBm. The uncorrected pulse is then described as having 76.1 – 75.2 = 0.9 dB overshoot with a
droop of 75.2 – 74.4 = 0.8 dB.
Measurement Considerations
Measuring pulsed radar signals requires a peak power sensor. For fast pulses, the rise time of the power sensor is important. The Boonton RTP5006 has a rise time of ≤3 ns. This means that a pulse rising edge of 5 ns can be comfortably measured.
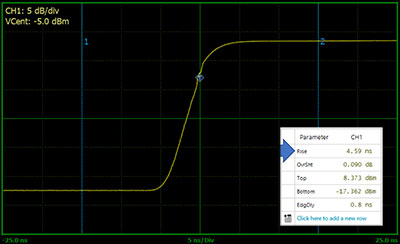
Fast real-time and equivalent-time sampling provide fine resolution on narrow pulses. The RTP5000 Real-Time Peak Power Sensors, with 100 MSa/s real-time and 10 GSa/s equivalent-time sampling, can make measurements on 10 ns pulses with 100 ps resolution. When measuring amplifier droop, automated measurements become important. Droop is one of the 16 automated pulse measurements available from the RTP5000 family.
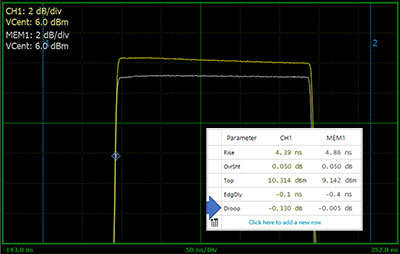
RTP5000 power sensors may be used with a PC running the Boonton Power Analyzer software or with the PMX40 Power Meter for a benchtop instrument experience. Either way, they provide the ideal tool to characterize radar and EW signals.
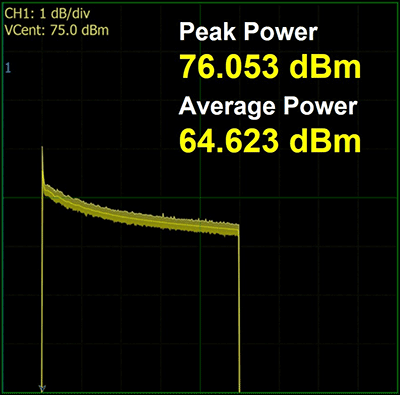
- Uncorrected 40 kW Pulse
- 500 µsec Pulse Width
- Peak Power 76.05 dBm
- Average Power 6436 dBm
- Rise Time 7 ns
- End of Pulse at 74.36 dBm
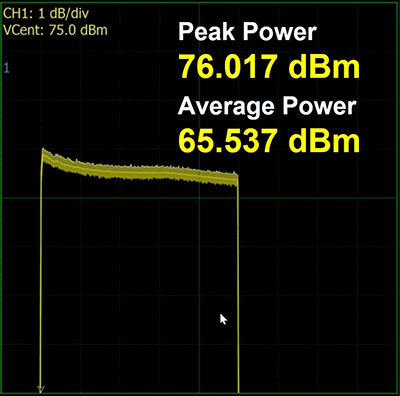
Figure 8: Results of applying the corrections
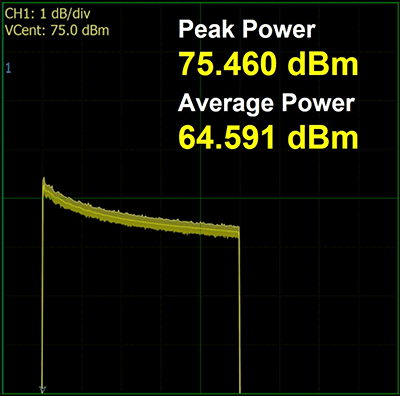
Adjust to maximum peak power by increasing system gain. This system gain is higher than the gain used in the uncorrected pulse example.
As shown in figure 8, the overshoot correction and the droop correction stages decrease the amplitude of the front of the pulse while the end of the pulse remains unchanged. The effect reduces the overall energy of the pulse, a poor tradeoff for generating a flat pulse. However, once the pulse is made flat, the gain of the system can be increased since the reduced overshoot will no longer trip the amplifier peak limiter. This is shown in figure 9. For the final result of Figure 9, the maximum peak power was adjusted by increasing the system gain. This results in a system gain higher than that of the uncorrected pulse example. For simplicity of illustrating the method, the gain adjustment has been described as the last step. In actual implementation, the correction factors are established ahead of time and stored, so setting the system to the optimized maximum gain is the first step. Next, the pulse rises and the overshoot is corrected with a final step of correcting the droop of the pulse.
Summary
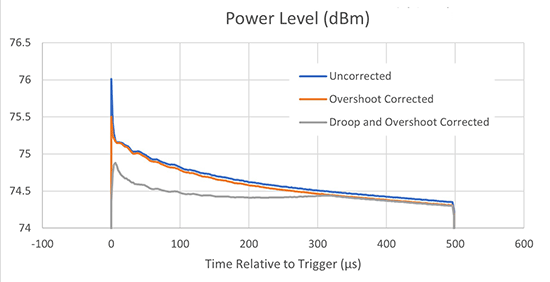
Reducing overshoot and droop allows for an increase in average pulse power while providing more uniform power throughout the pulse as shown in figure 10. The amplifier generates higher average power due to two factors. The gain, and therefore the output power, is set higher since the missing overshoot will not trip the output peak power protection. The average power is also higher because the droop is flatter.
Recap: Uncorrected Pulse
- Pulse peak power: 76.0 dBm
- Average power: 64.6 dBm
- End of the 500 µsec pulse: 74.4 dBm
- Total pulse variation: 1.6 dB
Recap: Pulse with Correction Applied
- Pulse peak power: 76.0 dBm
- Average power: 65.5 dBm
- End of the 500 µsec pulse: 75.4 dBm
- Total pulse variation: 0.6 dB
Conclusion
Using these techniques increased the average pulse power by 0.9 dB, which is close to the amount of pulse correction. This is as expected since the maximum transmitter output can be increased by the amount that the pulse variation is reduced. The result represents more than a 20 percent increase in average power, which also improves SWaP, cost and MTBF. The transmitter power density improves by 20 percent. The MTBF and cost improve since the component count in the RF chain would have been higher and the transmitter would have operated at a higher temperature to produce the 20 percent output power increase that would have been required without the pulse correction. In addition, the radar performance improves as roughly 1 dB of increased transmit power extends the range of the radar by 6 percent




